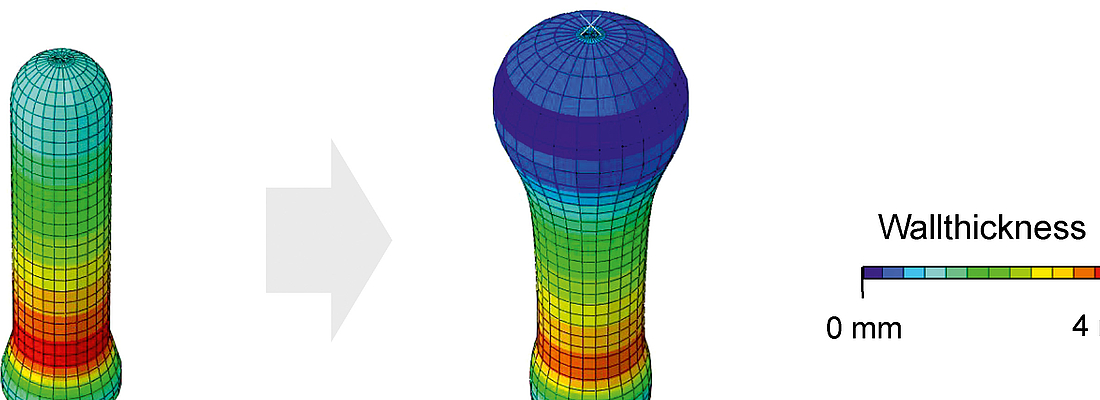

At the Institute of Plastics Processing (IKV) at RWTH Aachen University, an ongoing research project is investigating to what extent the stability of stretch blow moulded hollow bodies can be improved with simulation tools by modifying the preform design and process parameters. The aim is to achieve an ideal wall thickness distribution with respect to the requirements of the bottle.
At the Institute of Plastics Processing (IKV) at RWTH Aachen University, an ongoing research project is investigating to what extent the stability of stretch blow moulded hollow bodies can be improved with simulation tools by modifying the preform design and process parameters. The aim is to achieve an ideal wall thickness distribution with respect to the requirements of the bottle.
The investigations focus on the two stage stretch blow moulding process, where hollow bodies are produced from injection moulded preforms by biaxial stretching using a stretching rod and pressured air [1]. Due to the high production volume of current stretch blow moulding lines (e.g. 80.000 bottles per hour [2]), even small cost savings in the production of a single bottle lead to significant cost savings throughout the entire process. The greatest economic potential lies in the saving of material with a share of 70 to 75 % of the bottles manufacturing costs [3]. The challenge in reducing the amount of material is maintaining the requirements of the bottle such as stackability. These properties are mainly determined by the material distribution of the hollow body [4], which in turn results from the preform geometry and the parameters of the stretch blow moulding process. An optimised wall thickness distribution can therefore compensate weak spots of complex bottle designs.
With the aim of a load optimised material distribution for an arbitrary design, a computer-aided optimisation routine of hollow bodies is being developed in an ongoing research project at the IKV. This is achieved by a simulation of the stretch blow moulding process which is coupled with a simulation of the topload behaviour of the bottle. These simulations are integrated into an iterative optimisation routine in which preform geometry and process parameters are changed with the goal of weight optimisation. The results which are described in this article are focused on the potentials and limitations of preform- and process parameter variations in combination with different optimisation strategies for the determination of an ideal preform geometry and corresponding process parameters.
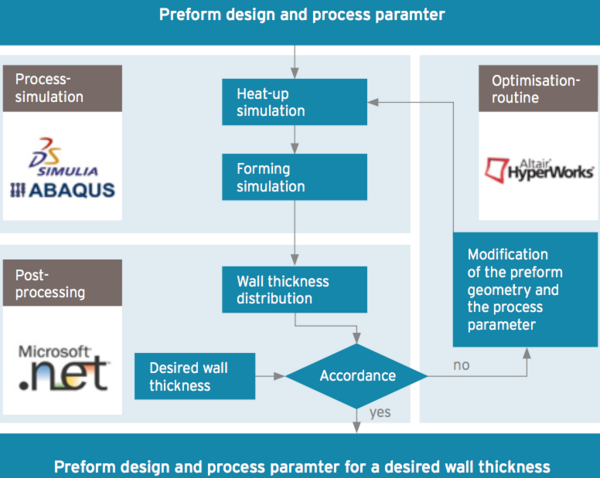
Fig. 1: Procedure of optimising the preform geometry and the corresponding process parameters
THE USE OF OPTIMISATION ROUTINES IN THE STRETCH BLOW MOULDING PROCESS
Optimisation is the determination of optimal parameters of a system by which a specified objective function is minimised or maximised. The aim of the optimisation is to locate the absolute optimum of a given function, in this case the maximum stacking load, within a defined range with as few calculation steps as possible [5]. There are various optimisation strategies for searching for maxima or minima of a certain system. These strategies can be divided into deterministic and stochastic methods for multidimensional optimisation problems [5]. Deterministic methods follow a fixed principle in order to change the parameter in each iteration. The stochastic optimisation methods use a random scheme that influences the search.
The procedure of optimising the preform geometry and the corresponding process parameters is shown in Fig. 1. At the beginning of the optimisation, initial values for the preform geometry and the process parameters are speci ed. These values are used for the simulation of the stretch blow moulding process and the topload behaviour. Both simulations are performed with the multi-purpose FEM software Abaqus, Dassault Systemes Simulia Corp, Rhode Island, USA. Intermediate calculations and the control of the simulations are processed by a software implementation in the programming language VB.NET of Microsoft Corp, Redmond, USA. The result of this simulation chain is the maximum topload of the bottle. The optimisation algorithm checks, if the maximum topload increased compared to the previous iteration. Roughly, if this is the case, further iterations follow and if this is not the case, the algorithm converges and the ideal preform geometry with corresponding process is found.
The simulation routines and the optimisation routine itself have many degrees of freedom. In case of the process and topload simulation, the accuracy can be increased by sophisticated material and process modelling. This increase in accuracy is usually associated with an increase in computing time. A very accurate simulation of the stretch blow moulding process and the topload can thus take about half a day on a computer server with multiple processors. If such a simulation is integrated into an optimisation routine, a calculation time of 50 days is required for 100 iterations. Therefore, the challenge is to determine a suitable trade-off between accuracy and computing time. In case of the parameter selection, almost any parameter of the two-stage stretch blow molding process and the preform geometry can be varied. In an optimisation routine, however, this leads to an increase in the number of iterations required to determine the best parameters for the objective function. Finally, there are various optimisation algorithms that lead to solutions of varying quality depending on the parameter space and the values of the objective function. Deterministic optimisation algorithms, for example, determine local maxima quickly using a quasi Newton method. However, there might be a better con guration of the parameter, the global maximum. Global maxima can be found, for example, by genetic algorithms. However, these algorithms require a lot of iterations and therefore a lot of calculation time.
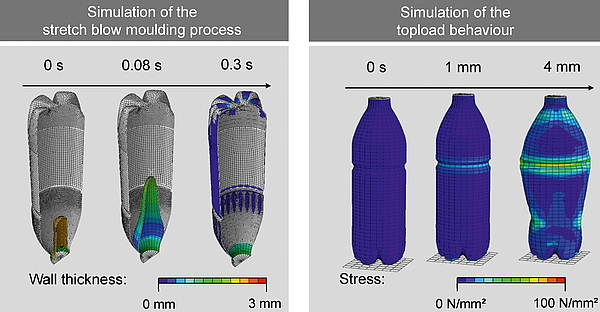
Fig. 2: Simulation of the stretch blow moulding process and the topload behaviour of a bottle
THE SIMULATION OF THE STRETCH BLOW MOULDING PROCESS AND THE SIMULATION FOR CALCULATING THE TOPLOAD BEHAVIOUR
The aim of the simulation is to calculate the maximum topload based on the preform geometry and the process parameters according to Fig. 2. The simulation of the stretch blow moulding process is exemplary illustrated on the left-hand side and the topload simulation is exemplary illustrated on the right-hand side.
An approach for the simulation of the two-stage stretch blow moulding process is a coupled simulation of the heating and the forming phase. Such a model was developed and successively improved in several research projects at the IKV [6, 7]. The deformation behaviour of PET is determined by a temperature and strain rate dependent hyperelastic Yeoh model. This model considers the material as isotropic. The coefficients of the material model are determined from stress strain curves of PET films in a stretching machine through equibiaxial stretching at different temperatures (90, 100, 110 and 120 °C) and strain rates (10, 50 and 100 %/s). The forming simulation, as shown in Fig. 2, models the interaction between the preform, pressurised air, the mould and the tip of the stretching rod. As an initial condition, the temperature pro le from the heating simulation is mapped on the preform. During the forming simulation, the preform is stretched through the stretching rod and a certain blowing pressure is applied to its inner surface. The coupled simulation of the heating and the forming process was validated in [6]. The result is shown in Fig. 3. The calculated wall thickness distribution in the area of the bottles body corresponds very well to the wall thickness distribution of experimentally produced bottles.
The simulation for determining the topload behaviour of PET bottles was developed in [6]. Equally to the forming simulation, the modelling of the material behaviour is decisive for the accuracy of the simulation. The material behaviour of stretched PET is strongly dependent on the stretch ratio. The Young’s modulus from undrawn, almost amorphous PET with ca. 2,9·109 Pa is compared to stretched semi-crystalline PET with ca. 14,9·109 Pa considerably lower [1]. The mechanical properties of PET are thus essentially determined by its internal structure (e.g. molecular orientation and degree of crystallization). The internal structures of the material are again changed to a large extent in the forming process by the stretching of the material. To take this behaviour into account, the mechanical characteristics are determined in dependence of the stretch ratio by the following procedure: Various stretch blow moulds, that differ in the diameter and height of the bottle, are used to produce sample bottles with de ned stretch ratios in the bottles body. These bottles are used to cut out specimen for tensile tests. The specimens are taken in height and in circumferential directions to determine the Young’s modulus in both directions in short-term tensile tests according to DIN EN ISO 527 [7].
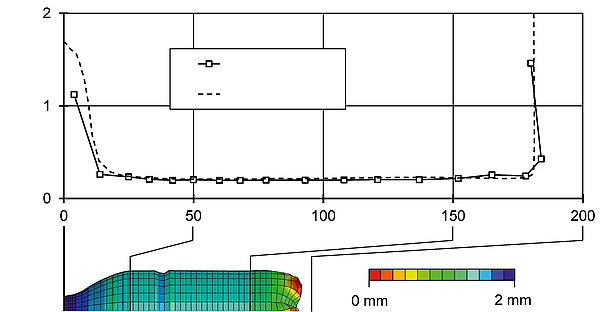
Fig. 3: Validation of the simulation of the two-stage stretch blow moulding process [6].
PARAMETERISATION AND DESCRIPTION OF THE OPTIMISATION ROUTINE
The result of the optimisation depends on the alterable parameters, the objective function and the optimisation algorithm. In the case of the bottle optimisation, the alterable parameters define the preform geometry and the process. In order to parametrize the preform geometry, the preform is divided into four zones according to Fig 5. Between these zones are the points 0 to 4 where the radius, thickness, height and temperature is de ned. The transition between these zones is linear. The process variables are the blowing pressure and the speed of the stretching rod that have a strong influence on the forming behaviour of the material. The speed of the stretching rod in stretch blow moulding lines is in most cases constant at about 1.5 m/s. The blowing pressure is applied in two stages. The preblowing pressure influences the deformation behaviour and is thus a parameter in the optimisation routine. The final blowing pressure is up to 40 bar and is used for the finished forming of the bottle. This pressure stage has only a minor influence on the wall thickness distribution and is therefore kept constant.
The optimisation is performed with the software MATLAB from MATLAB Corp., Natick, United States. The results described here were obtained using the deterministic inner-point method and a genetic algorithm. The inner- point algorithm varies each parameter by a small value at the beginning of the optimisation and checks whether the objective function improves. The parameters are then changed proportionately in the direction of the improved objective function. In a genetic algorithm selective random parameter sets are generated and changed by so-called mutation, recombination and selection [5].
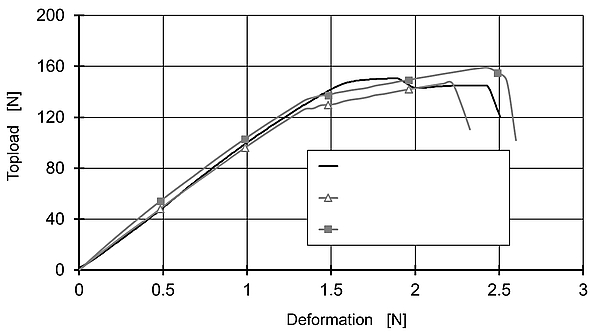
Fig. 4: Comparison of the topload at constant deformation speed between simulations and experiment
APPLICATION OF THE OPTIMISATION ROUTINE IN THE TWO-STAGE STRETCH BLOW MOULDING PROCESS
In a first investigation, the wall thicknesses at positions 1, 2 and 3 in g. 5 are alterable parameters of the optimization routine. The wall thickness in the tip of the preform at position 4 is set equal to the wall thickness at position 3. The preform temperature is set to 115 °C with the exception of the tip, where the temperature is set to 70 °C. Furthermore, a constant preform weight is specified as the boundary condition in order to prevent the improvement of the maximum topload through a higher preform weight that is perpendicular to the goal of material savings. The fixation of the preform weight leads to a reduction of the wall thickness at least one point (Fig. 5) if the wall thickness is increased at one point. This results in a large amount of local maxima of the objective function and thus the topload reaches a local maximum after a few iterations. Unfortunately, this value is below the initial value. According to this results, the weight limit is removed and the optimisation is performed again using the inner-point method and the genetic algorithm to check if the weight limit is the cause of the failed optimisation. The simulations during the application of the genetic algorithm failed in more than 90% of the iterations, because the wall thicknesses varied while the preform temperature is at a constant value. This causes areas with a very thin wall thickness to expand rapidly, as shown in Fig. 6, and the bottle is shaped incompletely. The results of the internal point algorithm without weight limitation are similar to those with weight limitation. In both cases, the optimisation does not lead to an improvement of the maximum topload, since the widely different wall thickness distribution in the preform in combination with a homogeneous temperature distribution leads to the creation of new weak spots of the bottle. Furthermore, the alteration of more parameters such as the height of the individual zones in g. 5 did not lead to an improvement.
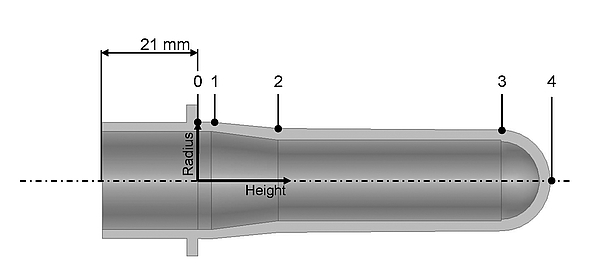
Fig. 5: Parameters for determining the preform geometry
The failures of the routines lead to the conclusion that an optimisation of the geometry without varying parameters of the process does not lead to an improvement of the bottles stability. In a further approach, the wall thickness and the temperature at position 2 are chosen as parameter for the optimisation, which was already a promising candidate for an improvement of the topload in previous optimisations. All other preform parameters are fixed. In addition, the preblowing pressure is set as a parameter. The optimisation is performed with the inner-point algorithm. The input preform is a 15.5 g preform for a 0.5 litre bottle. The initial values are a wall thickness of 2.43 mm, a temperature of 115 °C and a preblowing pressure of 2.5 bar. The objective function is the maximum topload, which was 114.72 N in the first iteration. Fig. 7 shows the change of the parameters in relation to the initial values.
The optimisation algorithm increases the wall thickness in the first step. The temperature remains at the starting level and the preblowing pressure is reduced. The optimisation leads to an improvement of the maximum topload and thus, an optimisation is possible with suitable parameters. The desired goal of weight minimization was not achieved in this run, as the optimised preform is heavier. However, the results show, that an optimization of the geometry and the parameters of the process lead to an improvement.
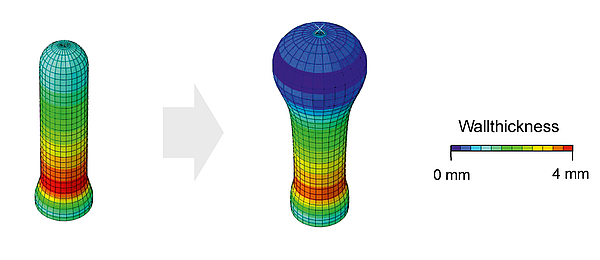
Fig. 6: Uneven preform deformation with homogeneous temperature control and very different wall thicknesses
CONCLUSION AND OUTLOOK
The first applications of an optimisation routine with the aim to improve the stacking strength of a bottle led to the conclusion that an optimisation of the preform geometry without altering the process parameters does not lead to an increase of the stacking strength. Further optimisations, that take the process parameters into account show promising results. Further approaches will focus on the application of a global optimisation by a genetic algorithm for determining a start parameters substitute for an optimisation by a deterministic algorithm. The global optimisation will be carried out with a simplified simulation model, which is similar to the model presented here. The deterministic optimization is carried out with the heating simulation and improved material models in the forming simulation and the structure simulation.
THANKS
The research project 19126 N of the Forschungsvereinigung Kunststoffverarbeitung was sponsored as part of the “Industrielle Gemeinschaftsforschung und -entwicklung (IGF)” by the German Bundesministerium für Wirtschaft und Energie (BMWi) due to an enactment of the German Bundestag through the AiF. We would like to extend our thanks to all organizations mentioned.
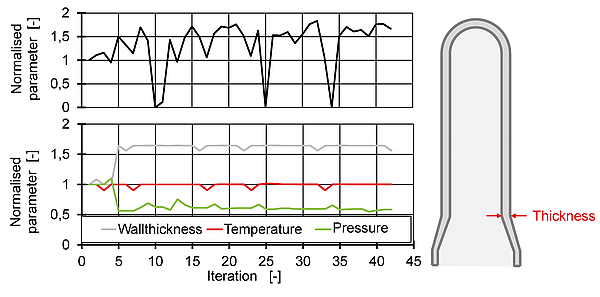
Fig. 7: Optimization for maximum topload with variation of the preform wall thickness and corresponding process parameters
The comPETence center provides your organisation with a dynamic, cost effective way to promote your products and services.

magazine
Find our premium articles, interviews, reports and more
in 3 issues in 2026.



